СИСТЕМЫ
ТЕХНОЛОГИЧЕСКОГО
МОДЕЛИРОВАНИЯ
Имитационное и математическое моделирование
Математическое моделирование
В процессе исследования реального объекта часто бывает нецелесообразно или даже невозможно иметь дело непосредственно с этим объектом. Удобнее бывает заменить его другим объектом, подобным данному в тех аспектах, которые важны в проводимом исследовании. Например, модель самолета продувают в аэродинамической трубе, вместо того, чтобы испытывать настоящий самолет - это дешевле. При теоретическом исследовании атомного ядра физики представляют его в виде капли жидкости, имеющей поверхностное натяжение, вязкость и т.п. Управляемые объекты являются, как правило, очень сложными, поэтому процесс управления ими неотделим от процесса изучения этих объектов. Один из способов изучения объекта – это получение новых знаний на основе исследования его модели.
Модель - это мысленно представляемая или материально реализованная система, которая, отображая или воспроизводя объект исследования, способна замещать его так, что ее изучение дает новую информацию об этом объекте.
Математическая модель - описание реального объекта с помощью математического представления (в виде системы уравнений, графов, операторов, функционалов и т.д.). Это один из вариантов модели как системы, исследование которой позволяет получать информацию о некоторой другой системе. Математическая модель предназначена предсказать поведение реального объекта, но всегда представляет собой ту или иную степень его идеализации (и упрощения).
Математическим моделированием называют как саму деятельность, так и совокупность принятых приёмов и техник построения и изучения математических моделей.
Формальная классификация моделей основывается на классификации используемых математических средств. Например, некоторые виды популярных классификаций моделей:
• по виду используемых в модели операторов: линейные или нелинейные;
• по подходу к описанию действующих закономерностей: детерминированные или стохастические;
• по виду функционирования во времени: статические или динамические;
• по описанию пространства состояний: дискретные или непрерывные.
и так далее. Каждая построенная модель является линейной или нелинейной, детерминированной или стохастической и т.д. Естественно, что возможны и смешанные типы.
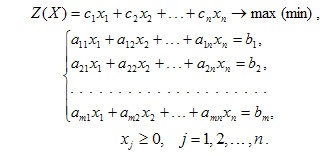
Пример. Математическая модель задачи линейного программирования
При моделировании используется аналогия между объектом-оригиналом и его моделью. Аналогии бывают следующими:
1. внешняя аналогия (макет самолета, корабля, жилого микрорайона, выкройка);

2. структурная аналогия (сеть промышленного трубопровода или электросеть моделируются с помощью графов, отражающих все связи и пересечения, но не длины отдельных участков);
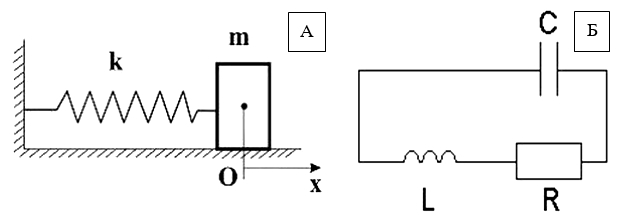
3. динамическая аналогия (аналогия функционирования системы во времени) – например, гармонический осциллятор (груз на пружине) (А) имитирует электрический колебательный контур (Б).
Имитационные модели относятся ко второму и третьему типу. Для них свойственно то, что они реализуются с помощью ЭВМ. Смысл имитационного моделирования заключается в том, что эксперименты проводятся не с реальной физической моделью объекта, а с ее упрощенной формой, пригодной для использования на ЭВМ, отражающей наиболее существенные взаимосвязи элементов системы, описывающей реальный объект.
С имитационной моделью производят вычислительные эксперименты: меняют те или иные показатели, т.е. изменяют состояние объекта и регистрируют его поведение в этих условиях. Основным достоинством имитационного моделирования является тот факт, что поведение объекта благодаря быстродействию ЭВМ имитируется во много раз быстрее, чем физический процесс протекает в реальности. Кроме того, вычислительный эксперимент, основанный на имитационном подходе, гораздо более дешев, чем реальный физический эксперимент, и может использоваться также и в тех случаях, когда натурный эксперимент труднореализуем по причине воздействия неустранимых внешних факторов.
Построение и сопровождение имитационных моделей стало неотъемлемой частью современного мира и повседневного процесса работы проектных организаций, являясь важным звеном в принятии оптимизационных и управленческих решений. Важной частью современного инжиниринга является совершенствование подходов к моделированию с целью повышения точности и детализации моделей, что обуславливает необходимость создания большого вариатива различных программных решений. Задача разработки более точных и быстродействующих программных реализаций различных моделей, является актуальной и имеет широкую практическую значимость.
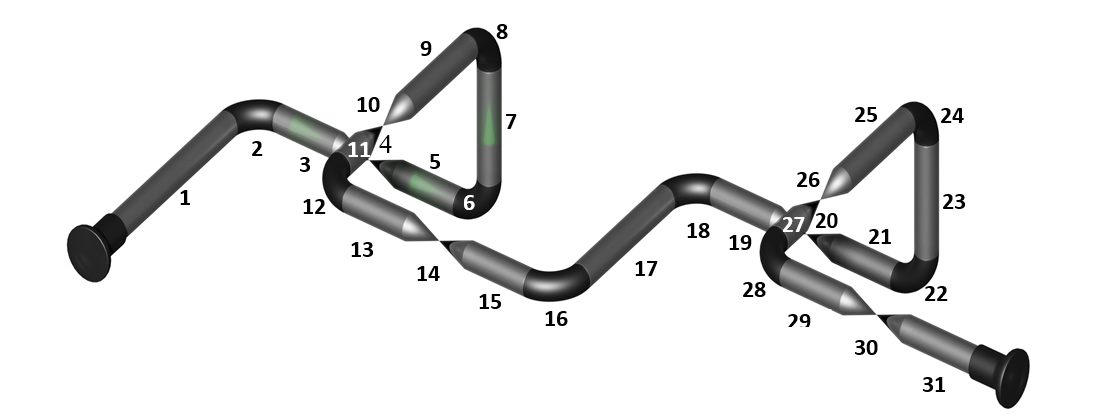
Пример имитационной модели участка промышленного трубопровода
Пример гидравлического расчета участка промышленного трубопровода
